在上一篇中，我們介紹了好幾種Learning Rate的調整方法和策略，我打算今天和明天再講解一些ML的基礎和做個小結，在第20天的時候，我們會進入Deep Learning的部分。

Perceptron原理

感知器（Perceptron）是機器學習中最早期的一種神經網路模型。它是一種二元分類模型，它接收多個二元數值並輸出「一個」二元數值。感知器的基本原理是模仿生物神經元的運作方式，通過對輸入信號進行加權總和，然後應用激活函數來輸出結果。

感知器的原理其實很簡單，它把接收的所有的輸入乘上各自的權重並進行加總，如果這個加總過後的值大於某個閾值，我們這邊稱它為threshold，就輸出1，小於這個threshold就輸出0：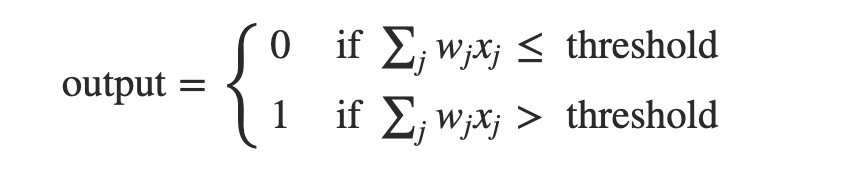

例子：
朋友邀請我去他的新家，我只會有兩種可能：去 或 不去，這樣的例子可以很好的用Perceptron來講解。
那麽什麽因素會影響我去或不去呢，這就是Feature，輸入。設：

• x1 = 當天不是颱風天（1=是， 0=不是）
• x2 = 當天有烤肉（1=是， 0=不是）
• x3 = 我前一晚沒有熬夜（1=是， 0=不是）

那麽對我來説，假如我的閾值設爲7，然後對我最重要的因素是當天不是颱風天，因爲如果是颱風天的話，我可能就沒辦法過去了，所以當天有沒有颱風對我來説非常非常重要，我給了他一個較大的權重為5。
同樣，作爲一個吃貨來説有沒有在他家烤肉也是對我來説很重要的事，因此我給了他一個權重4；如果我前一晚熬夜，可能會導致我隔天太過勞累，所以我給第三個條件的權重為3。

如果：
當天不是颱風天，且有烤肉，但是我前一晚熬夜了，我的總值會是：5*1 + 4*1 + 3*0 = 9 > 7，所以我的output等於1=>結論就是去。

化簡公式

輸入向量 x 和權重向量 w 之間的關係可以通過內積來表示，輸入的每個元素 x_i 都會與對應的權重 w_i 相乘，然後將所有結果相加，形成一個加權總和。這個操作可以更簡潔地表示為兩個向量的內積 w ⋅ x：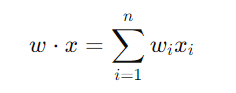

當加權總和超過這個閾值時，模型輸出Class 1，否則輸出Class 2。這個過程可以表達為不等式：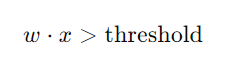

為了簡化這個表達式，通常會將threshold移到不等式的左邊，並表示為一個負的閾值，即：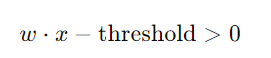

這樣的表達方式還可以進一步簡化，將threshold視為一個偏置項（bias），並用符號 b 來表示。因此，新的表達式變成：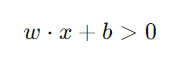

這是化簡過後的完整式子：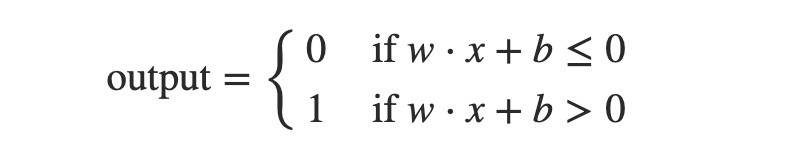

缺點

但是就如同其他的綫性模型一樣，Perceptron的局限性也很大，如果偏置項 b 是一個非常大的正數，則即使w⋅x是一個很小的數值，加上這個大的偏置後，整個輸入值 w⋅x+b 仍然會是一個正數。這意味著無論輸入 x 如何變化，神經元幾乎總是會被激活，輸出為 1。反之亦然。

這說明了感知器的一個局限性，當偏置項的值過大或過小時，輸出的靈活性會大大減少。這也揭示了感知器的另一個重要限制，即它只能處理線性可分的問題。當問題不能用一條線性邊界來分割時，單層感知器無法有效解決。